Consideration of Load Spectra in Transmission Design
For optimal gear design in accordance with requirements, it is essential to consider load spectra under the most realistic conditions possible as early as the virtual basic design phase. This is the only way to ensure that all components are loaded as evenly as possible to avoid overdimensioning.
Optimized design saves resources and costs and improves the CO2 balance – an aspect that is becoming increasingly important in the current environment and can offer a competitive advantage. Load spectrum calculations are also important for replacing complex time and cost-intensive experiments by simulating test rig damage tests.
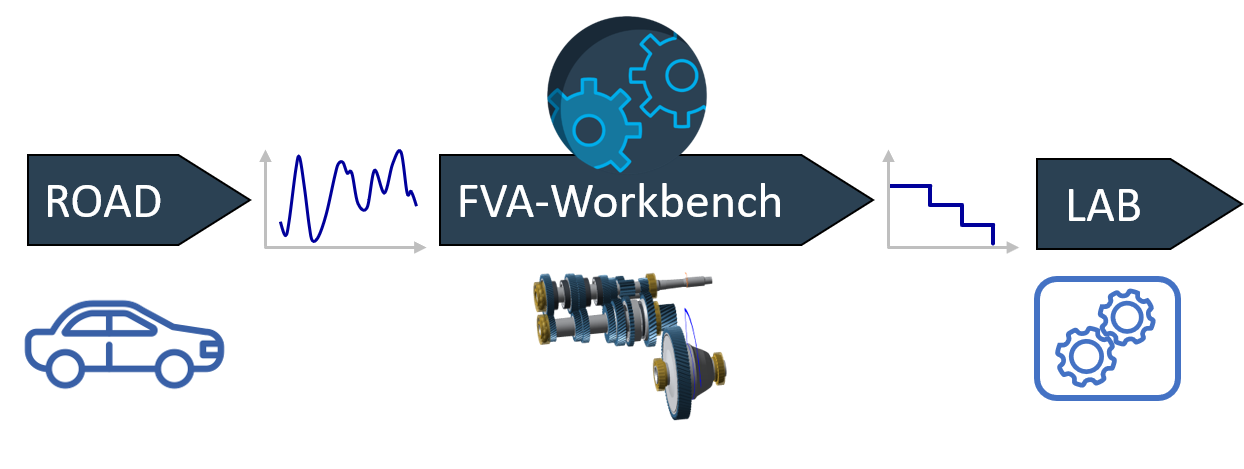
FIGURE 1: example application, substituting driving tests with bench tests
Creating load spectra
The FVA-Workbench offers extensive options for creating load spectra. For example, load levels (speed, torque, frequency) can be input manually or imported directly from a .csv file.
If load spectra are not available, synthetic load spectra can be created for initial analyses and preliminary designs. There are also a number of options for determining load spectra, for example from measurement data of single or multiparametric time level counts, or by creating a rainflow matrix. For bench tests, test times can also be reduced by omission and truncation, as long as the type and amount of damage are kept as similar as possible. These methods are based on the results of FVA Project Series 485 (LDA+).
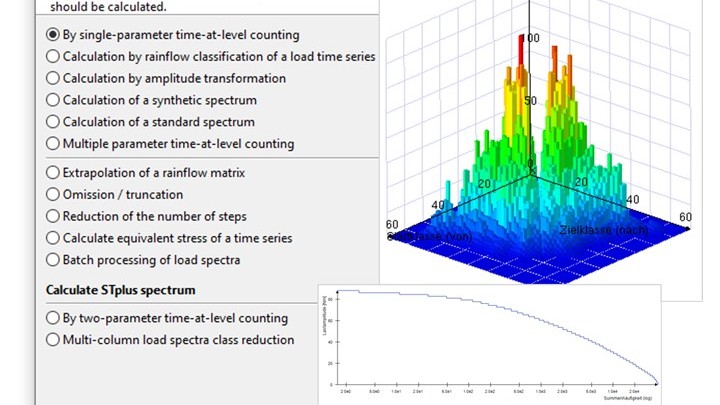
FIGURE 2: creation and processing of load spectra in the Global Database
Calculation options
Load spectra can be considered for the following components and calculations in the FVA-Workbench system calculation:
- For cylindrical gears, the flank and root load capacities can be determined according to ISO 6336-6: 2006 and 2019 based on load spectra. The spectrum safety factor according to Miner, the static safety factor, the fatigue safety factor, and the maximum permissible scaled total number of load cycles are all calculated. The gear excitation over the load (i.e., transmission deviation and excitation level) can also be calculated according to FVA 338 I:2001.
- For bevel gears, the focus is also on the flank and root load capacity according to ISO 10300:2014 or ANSI/AGMA 2003-C10. Spectrum safety factors against scuffing damage and micropitting are also determined, so that the respective locally solved critical damage cases can be represented over the tooth flank.
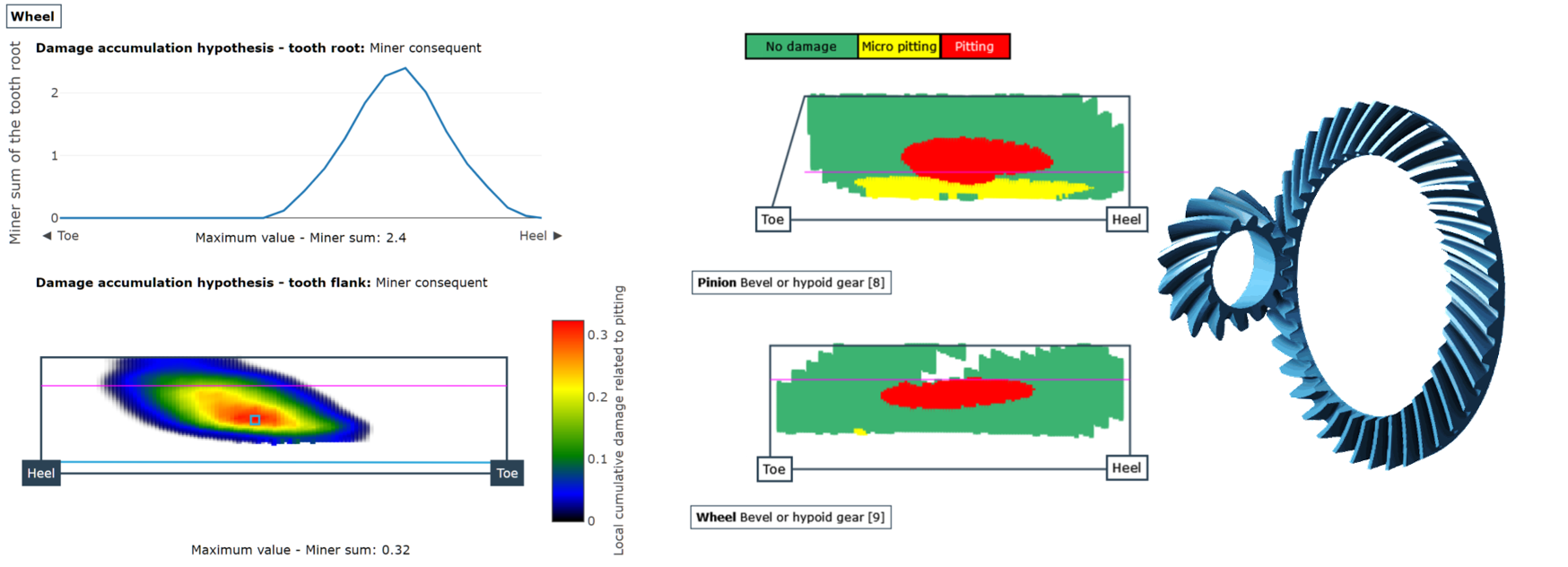
FIGURE 3: cumulative flank and root damage
For rolling bearings, the cumulative service life is calculated according to ISO 281:2007, SKF:2018, SCHAEFFLER:2018, or TIMKEN:2011. For shafts, load spectra are also considered for the calculation of the notch safety factors according to FKM:2012. This provides an overview of the influence of the load spectrum on all of the important main gearbox components.
Results output
Comprehensive report templates are available for outputting results, with ready-made tables and graphics. There are graphical outputs of the stress spectra for cylindrical and bevel gears, for both the tooth and root, and for each left and right flank.
In Figure 4, the calculated stress spectrum, for which the spectrum safety factor, the damage, and the static safety factor have been calculated, is shown in green. The spectrum is shown scaled to the load or stress in red, with maximum permissible cumulative damage up to 1. This calculation can be helpful for determining how much the load can be increased before damage occurs.
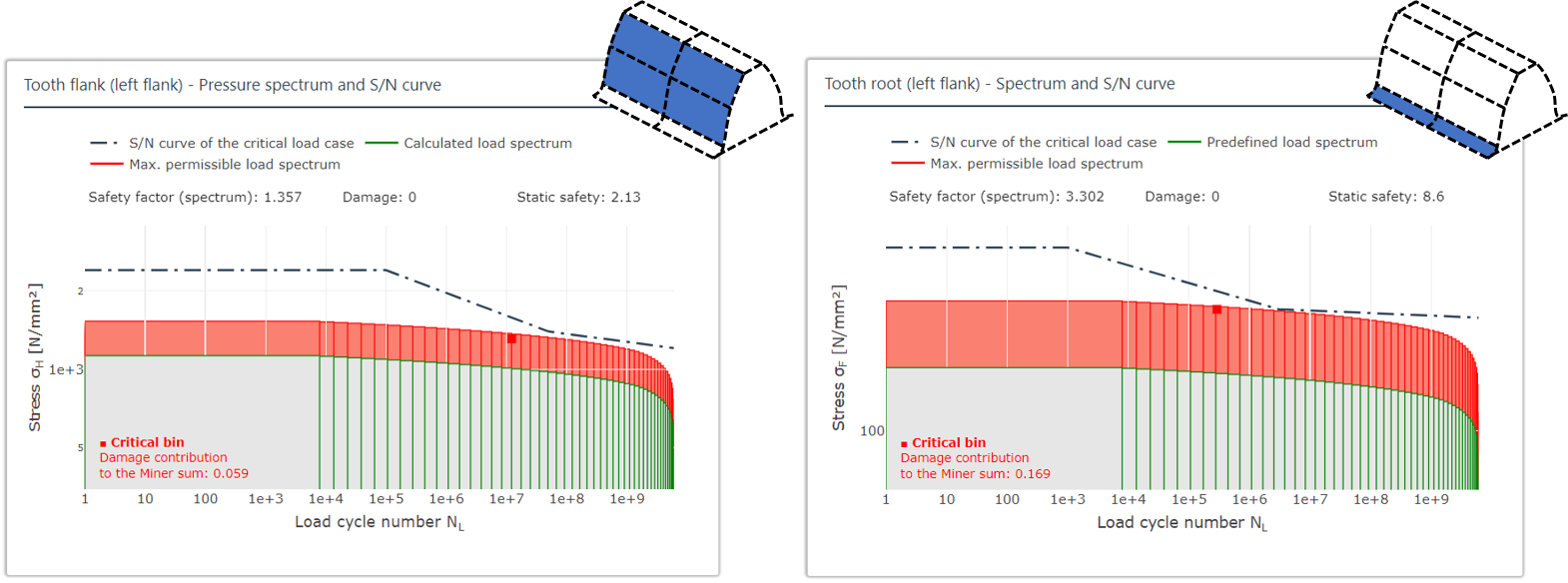
FIGURE 4: stress spectrum for the left tooth flank and root with cumulative safety factors
Calculation example
The example of a manual transmission is used to show the influence of different load spectra on the flank and root safety factors of the gears according to ISO 6336. Figure 5 focuses on the final gear ratio at the differential, which requires special attention during the design. This cylindrical stage is subjected to a wide range of stresses in each gear: from very high loads at comparatively low speeds and running times in first gear, to low loads at very high speeds and long running times in sixth gear. The reverse gear also loads the rear tooth flank.
This leads to conflicting design objectives and trade-offs: between the flank and root load capacity in the macrogeometry design, and with helix angle modifications for a centered contact pattern for the different operating points in the microgeometry design.
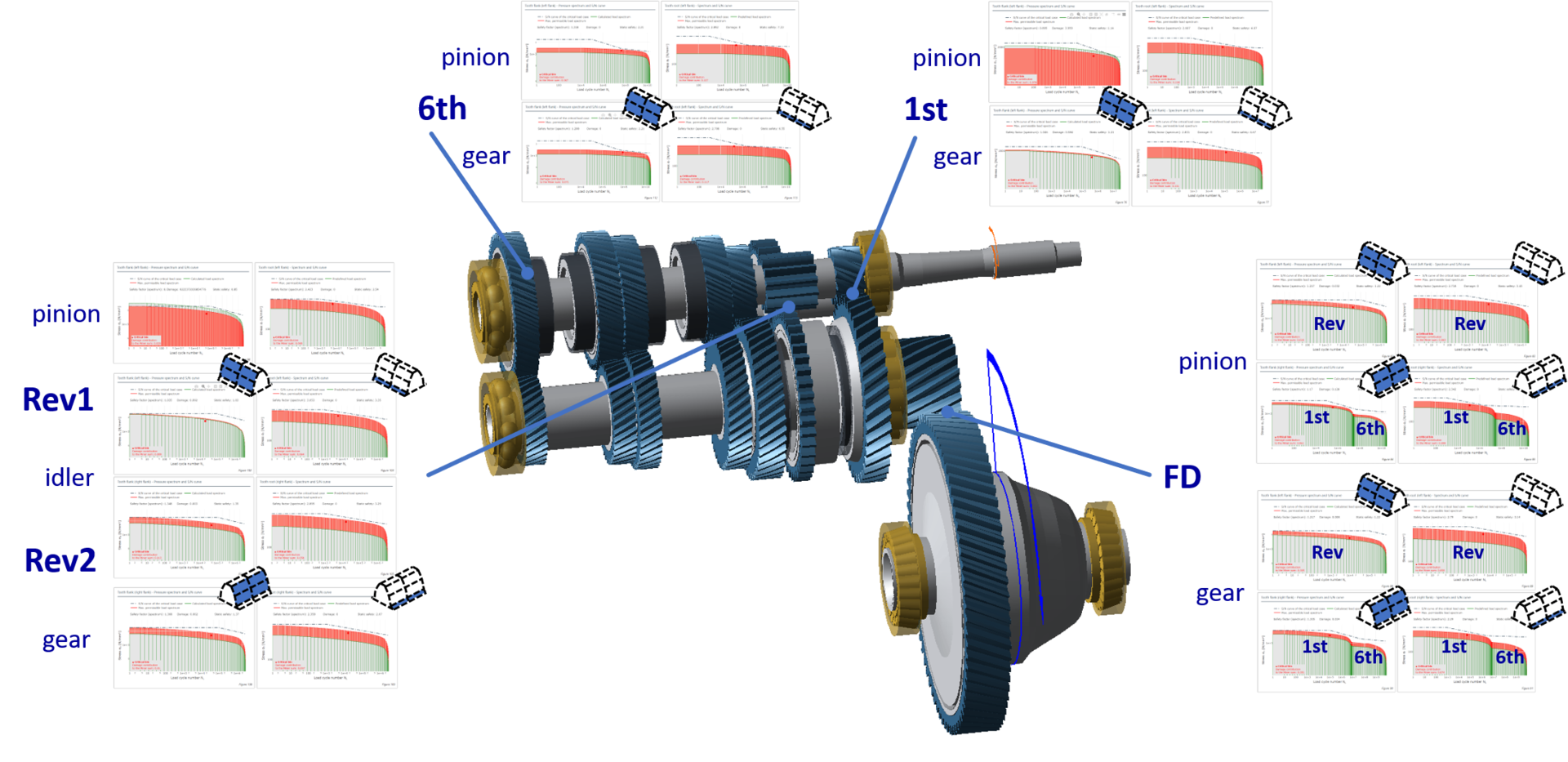
FIGURE 5: ISO 6336 results for the first, sixth, and reverse gears of a manual gearbox
The results shown here only include the gears and load cases mentioned above to better illustrate their effect on the final gear ratio. The different loads can be seen on the right flank of the ring gear for the first and sixth gears, and on the left flank for the reverse gear.
A fully defined calculation for this gearbox would include all six gears and reverse gear in driving load conditions during acceleration of the vehicle, and in coast load conditions during deceleration. With 50 load cases per spectrum, this results in (6+1)*2*50 = 700 individual calculations. All of these loads on the gearbox components can be calculated with a single calculation.
Conclusion
The FVA-Workbench can be used to quickly and easily analyze the influence of different load spectra on the safety factors of the most important gearbox components. The software also includes comprehensive methods for creating and processing load spectra.
References
[1] FVA Research Project 485 I to VI – Component Lifetime Calculation (LDA+ Subroutine)
[2] FVA Video Tutorial – Calculation of Load Spectra with the FVA-Workbench,
https://www.fva-service.de/en/software/tutorials/
[3] FVA KnowledgeBase – Load Spectra
https://doc.fva-service.de/70/knowledgebase/en/lastkollektive.html

